遠点、近点とは何か?それぞれ正視・近視・遠視における遠点・近点と、明視域について解説します。特に、遠視における遠点が勘違いが起きやすいと思うので、細かく書いていきます。
かなりの長文なので、ごゆっくりご覧ください。
正視・近視・遠視とは何か?という方はこちらから↓
遠点・近点とは
遠点
遠点とは、
- 無調節状態で網膜中心窩に結像する外界の点
- =無調節(自然の状態)でピントが合う位置
のことをいいます。調節に関しては別記事で詳しく紹介しますが、簡潔に言うと「より近くを見ようとするときに起こる目の反応」です。
詳細はこちら↓
「網膜中心窩に結像する」は、「ピントが合っていて明瞭に見える」という意味です。「調節がない状態」は、「自然な状態」、「その人の目の近視・遠視・正視などの状態」というイメージです。
近点
近点とは、
- 最大調節下で網膜中心窩に結像する外界の点
のことをいいます。できるだけ近くを見ようとしたときにはっきり見える近くの距離が、近点です。
はっきり見えるところがないパターンもあります。(遠視の遠点、遠視の近点の一部)
遠点・近点の求め方
遠点の求め方
無調節の状態でのピントが合う位置=遠点
つまり、本来の目の度数そのままから計算して求めた点が遠点です。
- 遠点=1/目の屈折値 (m)
となります。以下で例をあげていきます。
遠点の計算例
-3Dの近視の場合
遠点= 1/(-3)= -33.3cm
マイナスの場合は、「目の前方」となります。つまり、眼前33.3cmが遠点=ピントの合う位置です。(=手元33.3cmが裸眼で見やすい目)
-5Dの近視の場合
遠点= 1/(-5)= -20.0cm
同様にして、眼前20.0cmが遠点=ピントの合う位置です。(=手元20.0cmが裸眼で見やすい目)
正視(0D)の場合
遠点= 1/0≒ 無限
同様にして、正視は無限の遠くがピントの合う位置です。(=遠くが裸眼で見やすい目)
+3Dの遠視の場合(※注意)
遠点= 1/3= 33.3cm
プラスの場合、「目の後方」となります。つまり、眼球後方33.3cmが遠点となります。
しかし「眼球後方にピントが合う」とは普通言いませんよね。
近視・正視の場合を考えると、「ピントが合っていたら明視できる」はずです。しかし、眼球後方は見ることができませんよね。眼球後方33.3cmと言うと、頭の大きさにより多少差があるかもしれませんが、後頭部の少し後ろくらいになると思います。
つまり、遠視における遠点は、計算上そこにあるとされるだけであって、現実的には存在しません。
遠点は、
- 無調節状態で網膜中心窩に結像する外界の点
です。そもそも遠視は、「無調節状態ではどこにもピントが合っていない状態」を指しますから、「網膜中心窩に結像する点はない」ということになります。
+5Dの遠視の場合
遠点= 1/5= 20.0cm
同様にして、眼球後方20.0cmが遠点となります。
度数による遠点の距離
-5D, -3D, 0D, +3D, +5Dの例を出しました。
0Dのときが無限遠という遠くの位置になり、Dの絶対値が大きいほど、眼前も眼球後方も近い距離になります。(5Dの場合20cm、3Dの場合33.3cm)
近点の求め方
最大調節下の状態でのピントが合う位置=近点
つまり、本来の目の度数から最大調節した分を加味して求めた点が近点です。
- 近点=
1/(目の屈折値-最大調節力) (m)
となります。
近点の計算例
以下の例では、最大調節力を4Dとします。(最大調節力は年齢などにより変わります。)

-5Dの近視で最大調節力が4Dの場合
遠点は-5Dをそのまま、近点は-5Dの近視の状態に4D分の近視化(マイナス方向)を付加した場所になるので
- 遠点= 1/(-5)= -20.0cm
- 近点= 1/(-5-4)= -1/9= -11.1cm
となります。
正視(0D)で最大調節力が4Dの場合
- 遠点= 1/0≒ 無限
- 近点= 1/(0-4)= -1/4= -25.0cm
+3Dの遠視で最大調節力が4Dの場合(※注意)
- 遠点= 1/3= 33.3cm
- 近点= 1/(3-4)= -1/1= -100cm
この場合、遠点は眼球後方33.3cm、近点は眼球前方100cmということになります。
+5Dの遠視で最大調節力が4Dの場合
- 遠点= 1/5= 20.0cm
- 近点= 1/(5-4)= 1/1= 100cm
この場合、遠点は眼球後方20cm、近点も眼球後方100cmとなります。
明視域・調節域とは

明視域とは、はっきりと見える奥行きの範囲のことを言います。調節域と似た意味になりますが、調節域は遠点と近点の距離のことを言います。
調節域は、遠点・近点が眼前の有限距離の場合、明視域と同じ意味になります。有限距離ではない場合、「明視できる」という意味において視ることができない範囲がでてくるので、明視域とはちょっとニュアンスが異なります。
近視の明視域
- 近視の明視域は、遠点も近点も眼前の有限距離であるので、遠点~近点の距離です。
例)-5Dの近視で最大調節力が4Dの場合
- 遠点= 1/(-5)= -20.0cm
- 近点= 1/(-5-4)= -1/9= -11.1cm
→明視域は眼前20cm~11.1cmとなります。
正視の明視域
- 正視の明視域も、遠点が無限遠で近点が有限距離なので、遠点~近点の距離です。(無限)
例)正視(0D)で最大調節力が4Dの場合
- 遠点= 1/0≒ 無限
- 近点= 1/(0-4)= -1/4= -25.0cm
→明視域は無限遠~眼前25cmまで。(遠点、近点の2点の距離的には近似的に無限になります)
遠視の明視域
- 遠視の明視域は、遠点は眼球後方になり、近点は屈折力によります。
例)+3Dの遠視で最大調節力が4Dの場合
- 遠点= 1/3= 33.3cm
- 近点= 1/(3-4)= -1/1= -100cm
→この場合、近点が有限距離になる分の調節力があるので、明視域は無限遠~眼前100cmとなります。(はっきり見える範囲という意味)調節域とすれば、眼球後方33.3cm~眼前100cmとなります。
例)+5Dで最大調節力が4Dの遠視の場合
- 遠点= 1/5= 20.0cm
- 近点= 1/(5-4)= 100cm
→この場合、近点も眼球後方(実在しない)になるため、明視域は存在しません。調節域という表現をすれば、眼球後方20cm~100cmとなりますが、明視域(はっきり見える範囲)という意味では存在しないと言ってよいでしょう。
無限遠の光はどこに結像するか?
まぎらわしくなるのはここからです。遠点の意味と間違えないようにしましょう。
遠点、近点は、それぞれ「無調節状態・最大調節下で網膜中心窩に結像する外界の位置」でした。「無限遠の距離の光がどこに結像するか」ではありません。意味が異なります。
「無限遠の光がどこに結像するか」に関しては
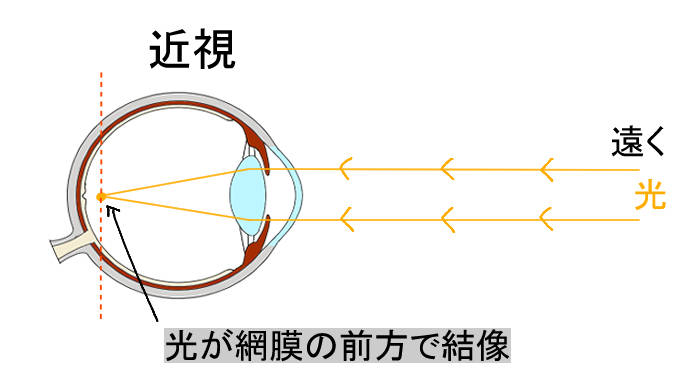
- 近視→網膜前方
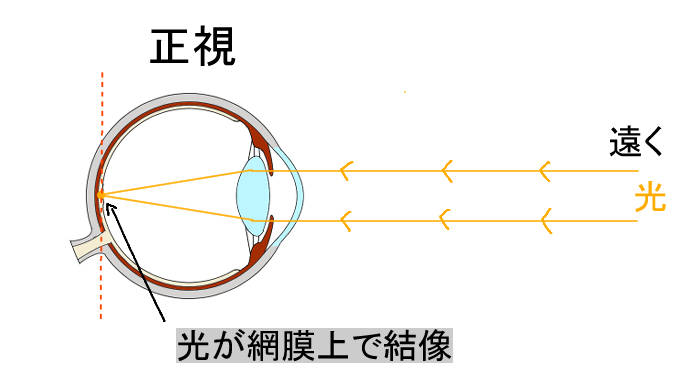
- 正視→網膜
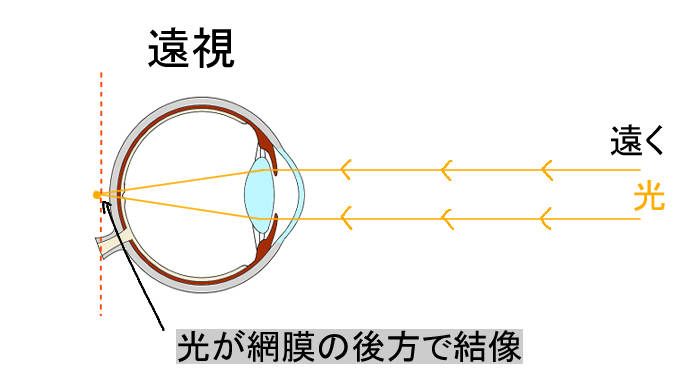
- 遠視→網膜後方
となりますが、遠視の場合は実際には眼球壁があるため、光は遮断され、網膜後方に結像することはありません。しかし眼球壁がない・もしくは眼球壁を通過すると考えれば、遠視は眼球後方に結像します。
「無調節状態で網膜中心窩に結像する外界の位置」に関しては
前半で述べてきた通り、
- 近視→眼球前方
- 正視→無限遠
- 遠視→存在しない(眼球後方)
となります。繰り返しになりますが「無限遠の光がどこに結像するか」と、「無調節状態で網膜に光が結像する外界の位置はどこか」では意味が異なります。ごちゃごちゃにしないように注意しましょう。
度数による無限遠からの光の結像位置関係
無限遠からの光と度数の関係
- 正視の場合は網膜上に結像します。(距離0)
- 近視の場合は網膜より手前に結像します。近視が強いほど、網膜からより離れた網膜前方に結像します。
- 遠視の場合は網膜より後方に結像します。遠視が強いほど、網膜からより離れた網膜後方に結像します。
先ほどの遠点と度数の関係は以下のようになります。
遠点の度数との関係
- 正視の場合、遠点は無限遠
- 近視の場合、遠点は眼前の有限距離にあり、近視が強いほど遠点は眼前から近い距離にある
- 遠視の場合、遠点は眼球後方にあり(実在しない)、遠視が強いほど遠点は眼球から近い距離にある
これを見るとわかるように、逆になるんですよね。二つは意味が異なるということがわかると思います。
遠視の遠点の考え方(参考)
昔、屈折や遠点などを考えた際に参考となったブログを紹介します。
- https://optkibebe.blog.fc2.com/blog-entry-1149.html 遠視眼の遠点|キベベワールド
こちらの記事を引用して要約します。
- 遠視は平行光線が無調節状態の目に入ったとき網膜より後方に結像する屈折状態
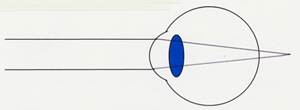
- 網膜後方に結像しているものを「調節」によって近視化させ網膜上に持ってきて見ることができる
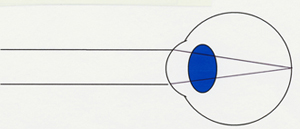
- 遠視の度数が強ければ強いほど、調節する力が強く必要となる
- +0.25Dの遠視の遠点は1/0.25= 4m、眼球後方4m
- +10Dの遠視の遠点は1/10= 10cm、眼球後方10cm
- +0.25Dの遠点の方が眼球後方4mと目から遠いのだから、網膜上に持ってくるためには+10Dよりも調節力が必要では?という疑問
- 遠視眼の遠点は、地球を一周した上での自分の後頭部を見ているイメージでの眼球後方の距離と考えるとわかりやすい
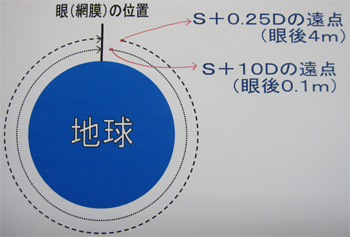
- こう考えると眼球後方4m(+0.25D)のほうが、距離としては短くなり弱い調節力で足りるとイメージできる
引用: 遠視眼の遠点|キベベワールド
というものです。イメージする上ではわかりやすい内容だと思いますが、注意点があります。
上の二つの目のイラストは、「無限遠の光がどこに結像するか」の絵で、この場合、遠視が強いほど眼球後方に結像し、網膜上に光を持ってくるためにはより強い調節力が必要となる、ということです。メガネで矯正する場合はより強い度数のメガネが必要となります。これは正しいです。(実際の目においては網膜後方に結像はしませんが。)
一方、下の地球のイラストは、「遠点」の話です。無限遠の光の話ではなく、「無調節状態で網膜に結像する外界の点はどこか」ということです。ですが、この場合だと、遠点を調節して網膜上に光を持ってくる話をしており、+0.25D(遠点=眼球後方4m)のほうが遠いから調節力が必要そうだ、と言っています。無限遠の光が網膜のより後方に結像している場合、それを調節して網膜面にもってくるにはより強い調節力が必要、であれば正しいです。
つまり、根本として二つの意味が違うということです。このことが分かると、この勘違いはなくなると思います。(この方が勘違いしているのではなく、こういう勘違いが一般に起きやすい、ということです。)
このブログ主はおそらくベテランのメガネ屋さんの方で、わかっていてわかりやすく書いていらっしゃるのかと思いますが、この点で勘違いしないようにご注意ください。そのほかにも眼光学・メガネの為になる記事がたくさん書いてあります。
調節力と明視域の計算例

調節力と明視域の計算例をいくつか出してみます。
調節力は
年齢による調節力
- 10歳で14D
- 20歳で10D
- 30歳で7D
- 40歳で4D
- 50歳で2.5D
- 60歳で1D
- 70歳で0.25D程度
- 80歳でほぼ0D
となります。調節力がどれくらいあるかによって明視域は変わってきます。また、近視の人はそもそもの遠点が近方なので、明視域という点ではそもそも狭いです。
正視の人で調節力が10Dの人の明視域は?
正視の人は無調節状態で無限遠にピントが合っています。(遠点=無限遠)
10Dの調節後は、近点は1/10=0.1m=10cmとなります。
つまり、明視域は無限遠~手元10cmであり、裸眼で遠くも良く見えるのでメガネは不要です。
近視-3Dの人で調節力が10Dの人の明視域は?
近視の人は無調節状態で近くにピントが合っています。(遠点=眼前の有限距離)
-3Dの人の遠点は1/3=0.33m=33cmとなります。(自然の状態で33cmのところが見やすい)
10Dの調節後の近点は、1/(3+10)= 0.077= 7.7cmとなります。
つまり、明視域は手元33cm~7.7cmとなります。近くはよく見えますが、33cmより遠くはぼやけて見にくくなりますので、メガネが必要です。
遠視+3Dの人で調節力が10Dの人の明視域は?
遠視の人は無調節状態でピントはどこにも合っていません。
遠視3D分を調節力3Dで打ち消して、ようやく正視と同じ無限遠にピントが合った状態となります。
※計算上は、遠点は1/3=33cm眼球後方に遠点があるといいます。
近点は残りの調節力7D分で考えればよいので、1/7= 0.14m =14cm手元に近点があります。
つまり、この人の明視域は無限遠~手元14cmとなります。
正視の人で調節力が4Dの人の明視域は?
先ほどと同様で、遠点は無限遠です。
近点は、1/4=25cmとなります。
つまり明視域は、無限遠~手元25cmとなり、その範囲が裸眼で見えます。
近視-3Dの人で調節力が4Dの人の明視域は?
遠点は1/3=33cm前方です。
調節力4D分を足すと、近点は1/(3+4)=14.3cmとなります。
つまり明視域は眼前33cm~14.3cmとなります。33cmより遠くはぼやけていきます。
遠視+3Dの人で調節力が4Dの人の明視域は?
遠点は計算上1/3=33cmで、眼球後方33cmとなります。
この人は調節力4D分のうち、3Dを使うことで自分の遠視と相殺させ、正視と同じく無限遠にピントを合わせることができます。
近点は残りの1Dを全て使った状態の位置になるので、1/1=1m 近点は眼前1mとなります。
つまり明視域は無限遠~眼前1mとなります。
1mより手前は調節力が足りないので、ピントを合わせることができずぼやけます。なので、近くを見るためにはメガネなどが必要となります。
これらのことから分かるのが、調節力が落ち着てくると、遠視の人は今まで見えていた近くが見えなくなることを強く自覚します。これが老眼です。一方近視の人も老眼はあるのですが(老眼は本来調節力が落ちた状態を指しますが、実際には近くがぼやけることを老眼といいます。)、元々遠くは見えないのでメガネをかけて生活していた、遠視よりは必要な調節力が少なく近くはよく見えるので、老眼は感じにくいです。
もう一つ例を挙げます。
近視-3D、調節力4Dの人で完全矯正メガネをかけている状態での明視域は?
上の近視の人がメガネをかけている状態での、明視域の考察です。
本来この人の遠点は33cmでしたが、メガネで完全矯正している(メガネをかけていると度数が0D=正視状態になっている)ので、メガネをかけた状態での遠点は無限遠です。その状態での調節力4Dですから、近点は1/4=25cmとなり、メガネをかけている状態では明視域は無限遠~手元25cmとなります。
つまりメガネで矯正している人は、完全矯正のメガネをかけた状態であれば、正視の人と同様な明視域となります。調節力がもっと落ちれば、たとえば2D程度になると近点は1/2=0.5m=50cmとなるので、50cmより手前は見にくくなり老眼を自覚します。
これは正視の人もそうだし、近視の人がメガネをかけている状態でもそうです。つまり近視の人もメガネをかけた状態であれば、老眼は自覚します。しかし近視の人はメガネを外せば元々近くにピントが合っているので、近くを見ることができます。
まとめ
- 遠点は無調節状態で網膜にピントが合う外界の点
- 近点は最大調節下で網膜にピントが合う外界の点
- 近視はどちらも眼前有限距離にある
- 正視は遠点は無限遠、近点は眼前有限距離にある
- 遠視は遠点は眼球後方(実在しない)、近点は調節力により眼球後方、無限遠、眼前有限距離いずれもある
- 明視域(調節域)は、遠点~近点の距離(遠視の場合は実在しないが計算上算出はできる)
- 無限遠からの光の結像位置の関係と、遠点との関係を勘違いしないように
以上、遠点・近点まとめでした。
遠視の遠点を考えるとドツボにはまる可能性があるので、そういうものだと暗記するのが良いと思います。この辺りは光の屈折関係の内容であり、完全に物理学の内容であり苦手な人は多いかもしれません。
同領域のおすすめ記事
以下の参考書は、この領域をほぼ網羅していると思われる良書です。ただし、わかりやすいかと言われると、少し難解な内容でもあると思います。(そもそも光学系が、ザ・理系以外にはやや難しいような気がします)
眼科医向け眼光学・屈折・調節の参考書





コメント
コメント一覧 (3件)
1/1=10cmとなっているところいくつかありますが、1mもしくは100cmです。
このサイトを読んで、とても理解が深まり助かりました、医学科6年卒業試験奮闘中の者です。
コメントありがとうございます。
該当箇所の修正いたしました。試験がんばってください!
ご返信いただき、ありがとうございますm(._.)m
プロフィールも見させていただきました。「卒業試験」が通じてよかったです笑
ありがとうございます、がんばります。卒試の合間に、ほかの記事も勉強させていただきます!
コメントの顔写真がおじさんになるんですね…^^; (女子です)